How I Reverse-Engineered Huge Excel File Full of Complex Formulas

In this article, I want to share an interesting experience. It has nothing to do with SAP Commerce and might even be unrelated to eCommerce, but it could be useful for Solution Architects when tackling a task similar to mine. And the task was interesting. And was part of a big e-commerce project.

It was a huge Excel file for generating estimates for B2B customers. A manager entered a bunch of parameters according to customers’ needs and get a printable quote. This Excel spreadsheet was really old, already about ten years old, and all these ten years, different people have been adjusting it, correcting it, adding formulas and constants. Basically, almost nobody knew how it worked in all details. All this evolved into a dozen tabs, each filled with numerous formulas. And these formulas refer to similar formulas from the adjacent tabs. It has almost a thousand formulas, mostly complex. How to untangle this knot?

There was no documentation, but even if there had been, where is the guarantee that the documentation fully matches the Excel file? After all, if it doesn’t match, finding the root causes of the discrepancies will be very difficult. Since the Excel file is the source of truth, it basically is the documentation.

The company’s manager would input data into a couple of dozen fields on tab X and then print the estimate from tab Y. The elements of this estimate were calculated through all these magical formulas. Moreover, for instance, the data from tab X determined how many rows would be in the estimate on tab Y and what rows from the big set of products are included there.

For understandable reasons, I cannot use the original file in this article, nor can I recreate a file of similar complexity, sorry. And it would be difficult to demonstrate the solution on it. But it’s important to understand that a simple file wouldn’t have required a solution. Simply put, in the case of a very complex Excel file, it was unclear how to even approach reverse engineering.

The following is a typical formula from a random cell from the file.

=IF($D11=$D10,"", IF(ISNUMBER( INDEX(Data!$T$10:$U$17, 
MATCH(TabCalc!$F11,Data!$T$10:$T$17,0),2)), 
INDEX(Data!$T$10:$U$17, MATCH(TabCalc!$F11,Data!$T$10:$T$17,0),2), 
INDEX(TabProd!$C$8:$U$112,TabCalc!$D11,I$1)))

I’m providing an explanation of what each part of this formula does, but in essence, it’s not important for what follows. Feel free to skip this if Excel formulas scare you or annoy you. I would skip it. Last time, there won’t be any more of them, I promise.

• IF($D11=$D10,””, …): This is the outermost IF function. It checks if the value in cell D11 is the same as the value in cell D10. If true, it returns an empty string (“”), meaning it does nothing if the two values are equal. If false, it proceeds to the next IF function.
• IF (ISNUMBER (INDEX (Data!$T$10:$U$17, MATCH(TabCalc!$F11,Data!$T$10:$T$17,0),2)), …): This is the next IF function nested inside the first one. It checks if the result of an INDEX-MATCH formula is a number.

• • The INDEX(Data!$T$10:$U$17, … ,2) function is looking up a value within the range $T$10:$U$17 on the ‘Data’ sheet. The row number to return is determined by the MATCH function.
  • The MATCH(TabCalc!$F11,Data!$T$10:$T$17,0) function is searching for the value in cell F11 on the ‘TabCalc’ sheet within the range $T$10:$T$17 on the ‘Data’ sheet, and returns its relative position. The ‘0’ specifies an exact match.
  • If the result of the INDEX function is a number, the ISNUMBER function returns TRUE.

• INDEX (Data!$T$10:$U$17, MATCH(TabCalc!$F11, Data!$T$10:$T$17,0),2): If the ISNUMBER check is TRUE, the formula returns the value found by this INDEX function (as described above).
• INDEX (TabProd!$C$8:$U$112, TabCalc!$D11,I$1): If the ISNUMBER check is FALSE, meaning the INDEX-MATCH did not find a number, this INDEX function is the alternative. It retrieves a value from the ‘TabProd’ sheet within the range $C$8:$U$112. The row number is specified by the value in cell D11 on the ‘TabCalc’ sheet, and the column number is specified by the value in cell I$1.

So, we need to do reverse engineering, but how can we make sure we haven’t made any mistakes in the process of translating the formulas? That’s right, during the research process, it’s essential to write the calculations immediately in a programming language. However, this needs to be done in such a way that it can be completed within a couple of weeks, and at the same time, not to mess up in the programming language itself.

But where to start? There are a lot of dependencies. Any randomly selected cell contains a reference to three others, and those three each refer to five more, with some two of those five being used in an adjacent calculation that also has dependencies. This leads to a rather disheartening scenario where the program will only work and produce some output if all formulas are transferred into it. Until then, it won’t work at all (actually, not exactly, read on).

The second problem is that the cells are not named. D11, T10, U17. Yes, formally, it is still a more or less organized spreadsheet, and each number that enters into the input data, as well as every calculated value, has a label in one way or another. And these labels have a hierarchy.

For example, in the same estimate, there’s a list of products, and each product has a price. One could say that the price has a label in the form of the product’s SKU or its position number in the estimate – all of this with a “price” suffix. And then there’s the quantity of this product, which is also calculated, and that cell would have a “quantity” suffix.

Essentially, it was necessary to find a programming language that would allow for describing the function for calculating the price of an item in the estimate as the product of the calculated quantity and the calculated unit price, but at the same time, not to implement the calculated quantity yet, leaving that “for later.” And when “later” comes, there might be another dependency to leave for later as well. However, in order for anything to be calculated at all, these dependencies need to be mocked with some temporary values taken from Excel. Gradually, we replace the mocks with real functions, and when there are no more mocks left, everything should work as intended and produce the same data as Excel does.

This approach requires a programming language or framework that supports a few key features:

• Lazy Evaluation: The ability to define functions and expressions that are not evaluated immediately but are instead evaluated when needed. This is crucial for defining calculations that depend on data or calculations that will be defined later.
• First-Class Functions: Functions that can be passed as arguments to other functions, returned as values from other functions, and assigned to variables. This allows for flexible composition of calculations.
• Mocking and Stubs: The capability to temporarily substitute real functions or calculations with placeholders that return predefined values. This is essential for developing and testing parts of the system in isolation.
• Refactoring Tools: Tools that help safely replace temporary implementations (mocks) with real ones without breaking the overall system.

On a side note: Frankly, talking about formulas, Microsoft Excel has a dreadful design. I mean, take their DSTDEVP function (standard deviation for an entire population with conditions). If you switch from a computer with English set as the system language to one where the interface isn’t in English, the formulas get names like this:
— English: DSTDEVP
— Spanish: DESVEST.PB
— French: ECARTYPEPB
— German: STABW.DB
— Italian: DEV.ST.P.DA
— Portuguese: DESVPAD.PB
— Russian: СТАНДОТКЛНУСЛ
Talk about making things complicated. Obviously, my French isn’t nearly good enough to translate DSTDEVP into ECARTYPEPB. I had my system in French to keep it fresh in my mind, but I switched it back to English because of these kinds of mess-ups, leaving French for just my phone. Oh, and let’s not forget that changing the language of Microsoft Office from the system language without some “hacks” isn’t possible. The hack involves physically removing the localization files for the system’s language from the Microsoft Office package, which then forces a fallback to English.

So, for the lazy evaluation and functional programming languages like Python, JavaScript, Ruby, and Groovy could be good candidates because they support these features to varying extents and their syntax is compact and clear.

Python and Groovy were both considered by me, but there were difficulties with accessing global data structures in Python modules and the code was as simple and clear as with Groovy, so I decided that Groovy managed to handle this quite well. Probably that is due to lack of my Python experience. So, I picked Groovy.

Let’s take a super simple example:

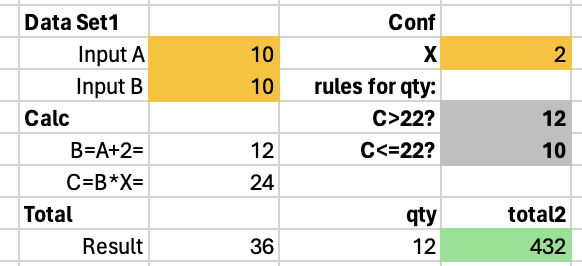
Cells marked in yellow are input data, like “to be entered by a manager”.

Grey cells are configurations that the manager might be able to adjust, but very cautiously.

All white cells are, ideally, protected; nothing in them should be altered. Some of these cells (where there are numbers) contain formulas. The data in them are intermediate and used by other formulas.

Green cells represent the final result. Data from these cells are not used by other formulas.

This is the main app — it prints the input parameters, calculations, and final results:

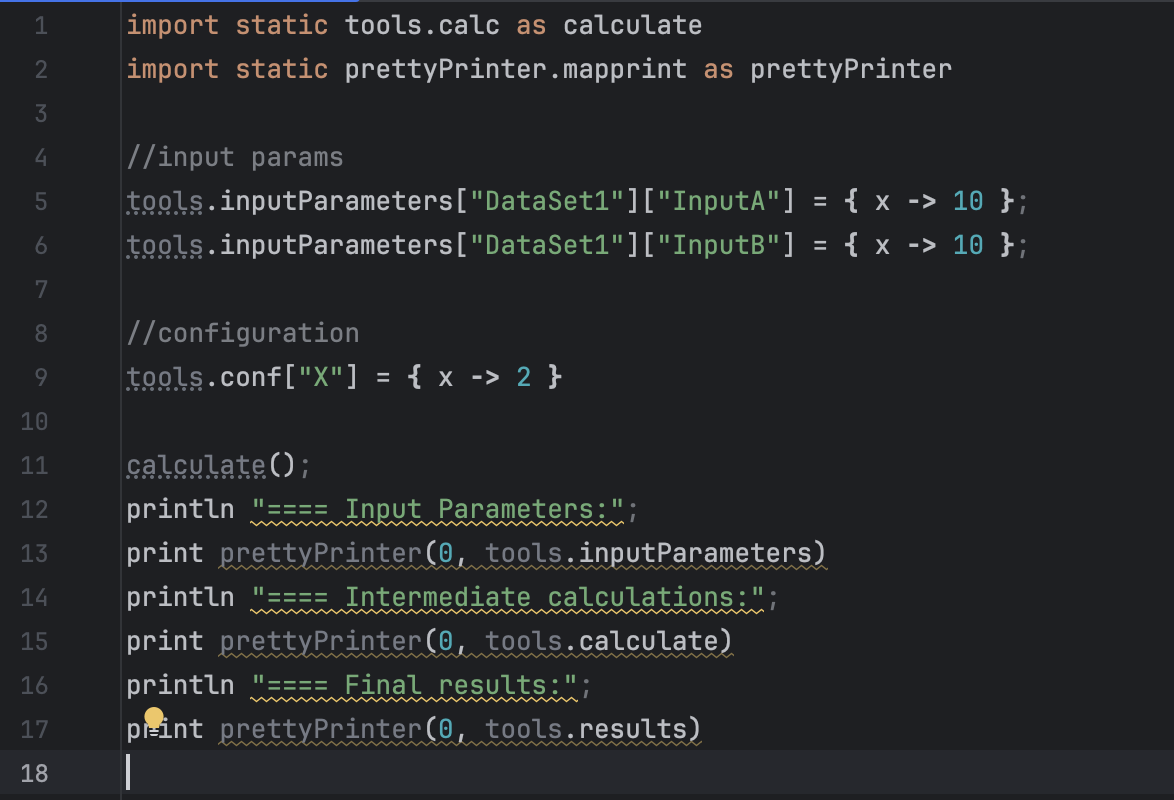
The calculations are defined in tools.groovy:

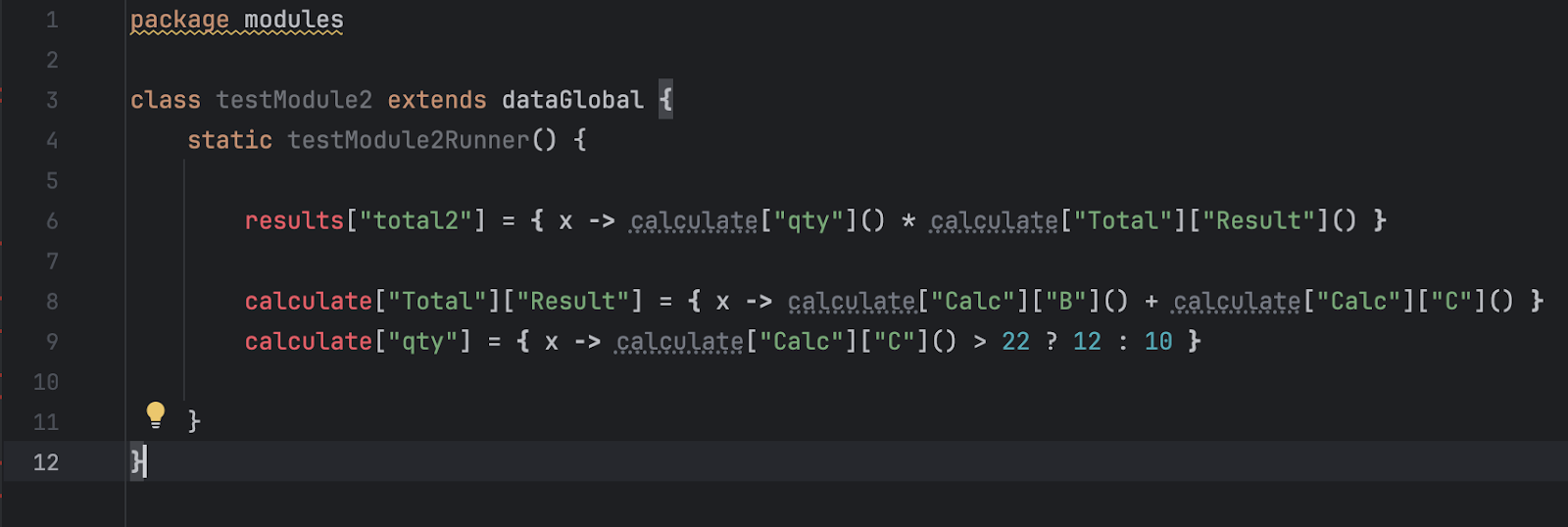
Let’s assume that B and C are not implemented yet, and create temporary mocks for them:

The rest will use these mocks:

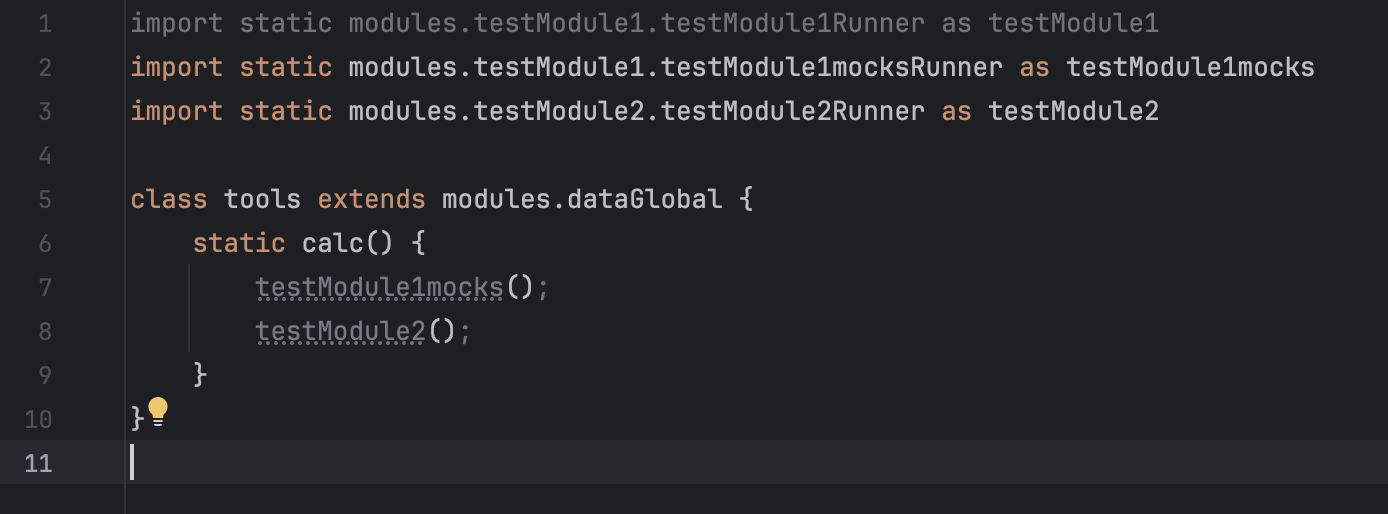
Basically, both modules define functions, but their names are dynamic and implemented as maps:

Basically it is why Groovy not Python. These static maps are used in all modules. In Groovy, it was easier to implement.

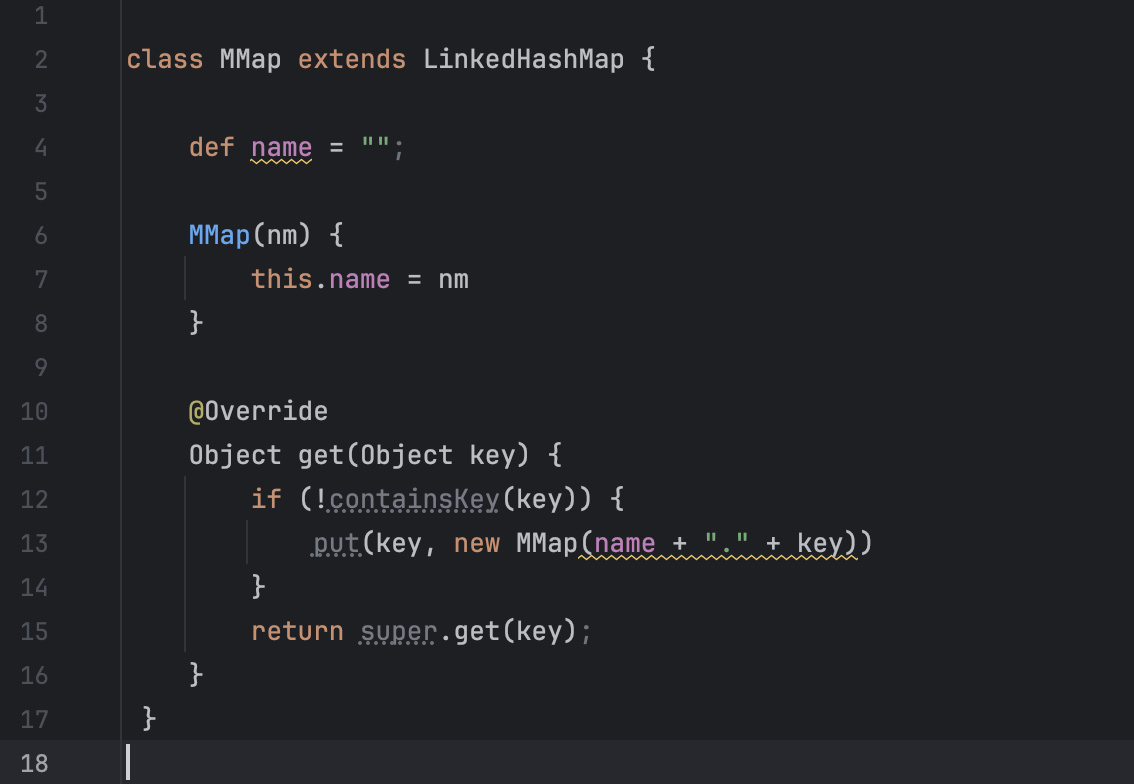
The MMap class inherits LinkedHashMap. It redefines a getter so that it could work with non-existent keys:

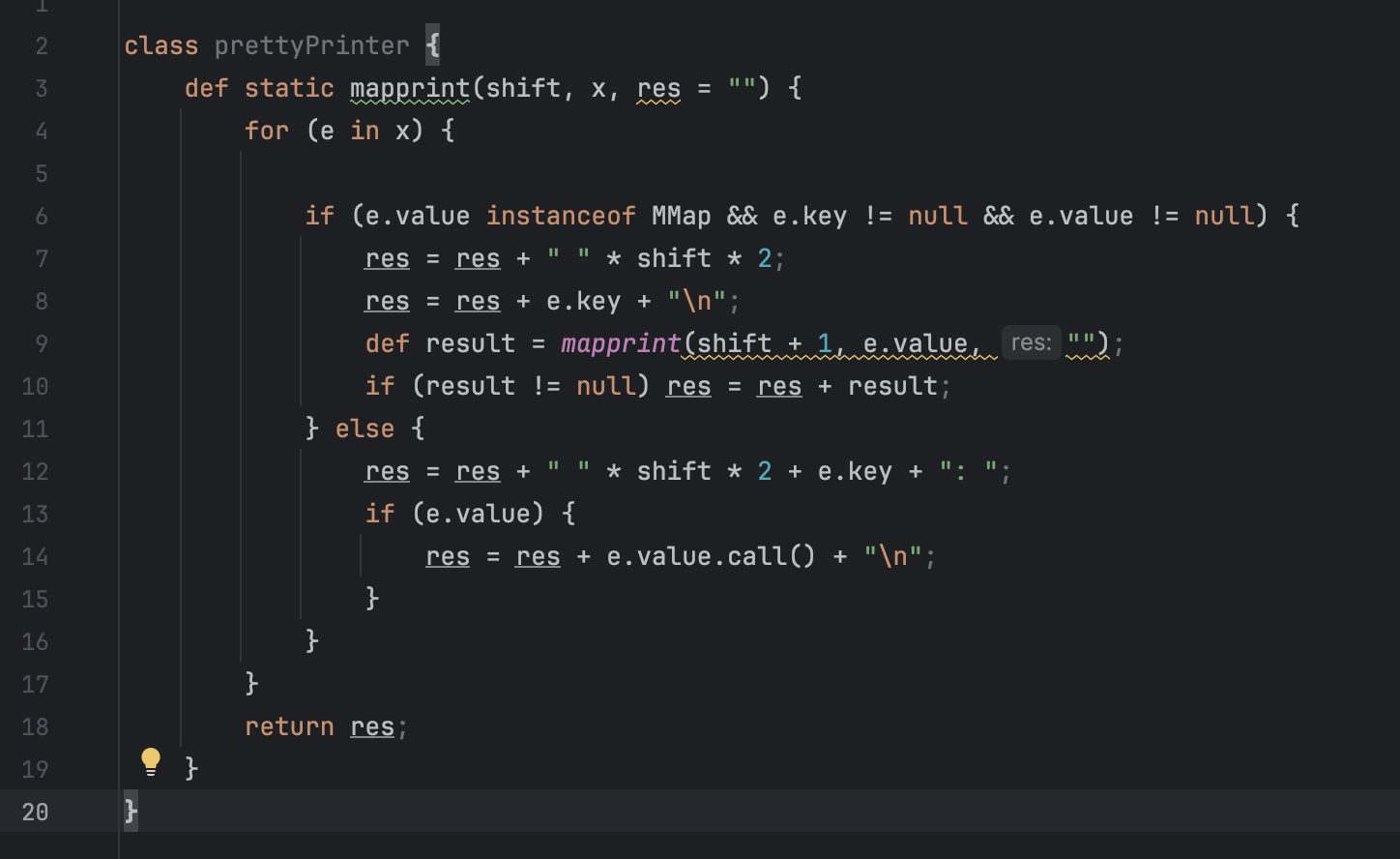
And the last one is prettyPrinter — we need for calculating and printing the results:

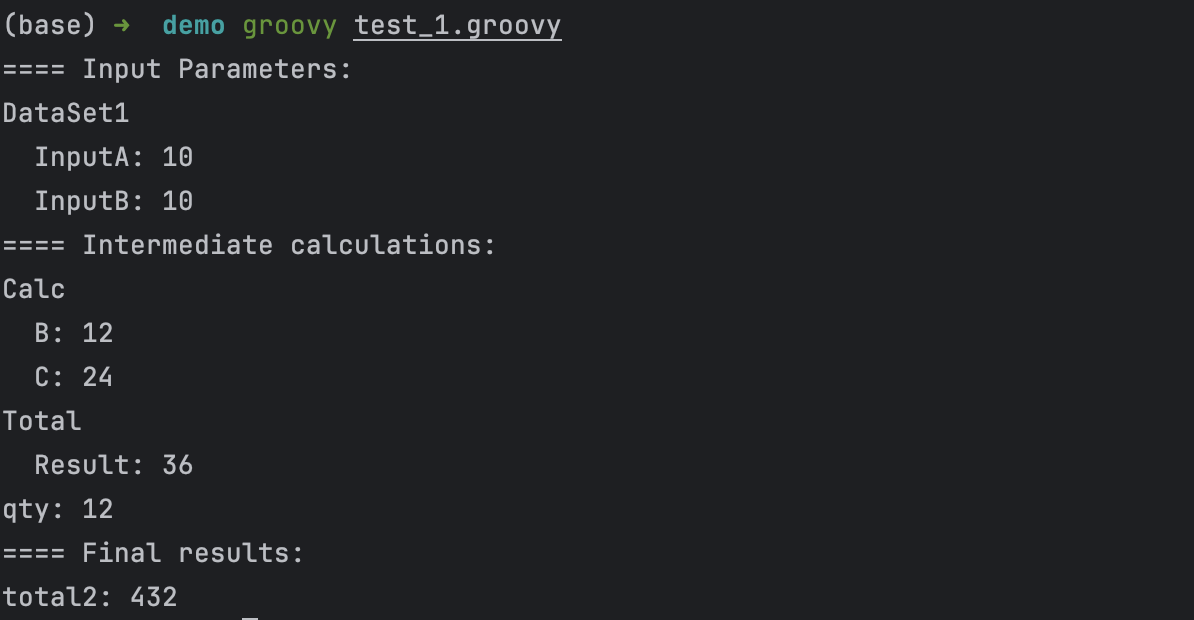
Let’s run our calculations:

We used mocks for B and C, right? Now let’s replace it with the actual implementations:

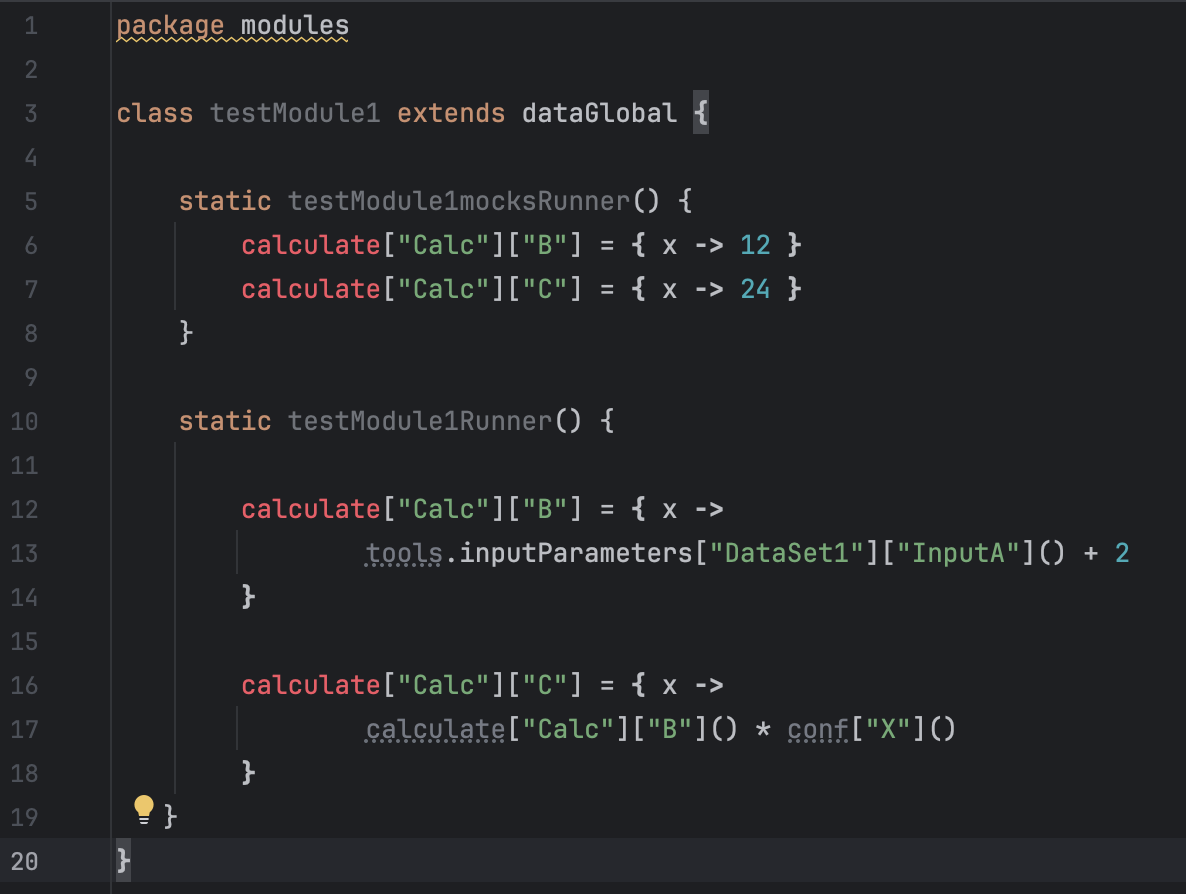
and remove “mocks” from testModule1:

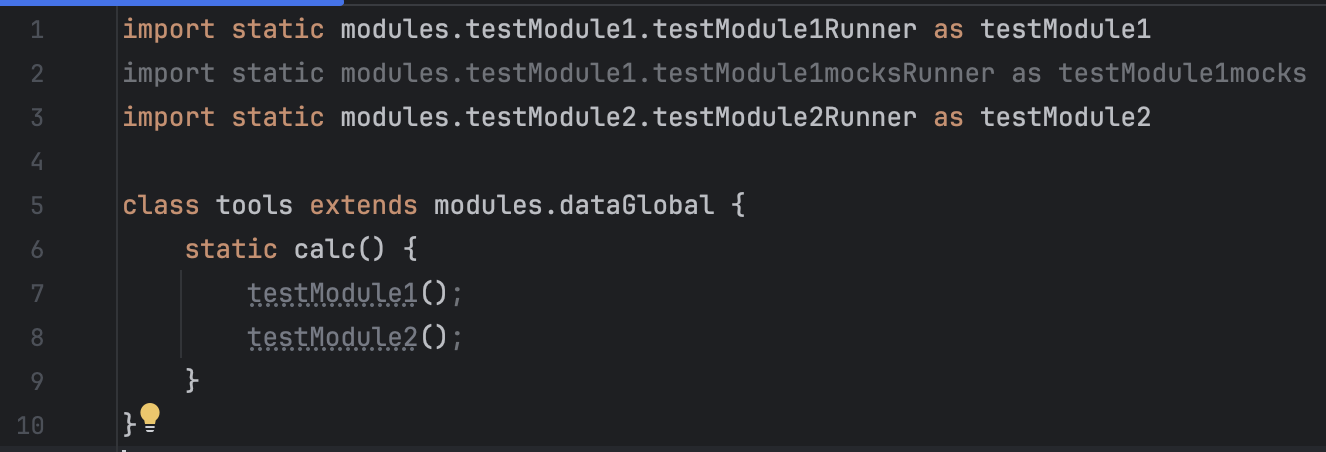
Run again:

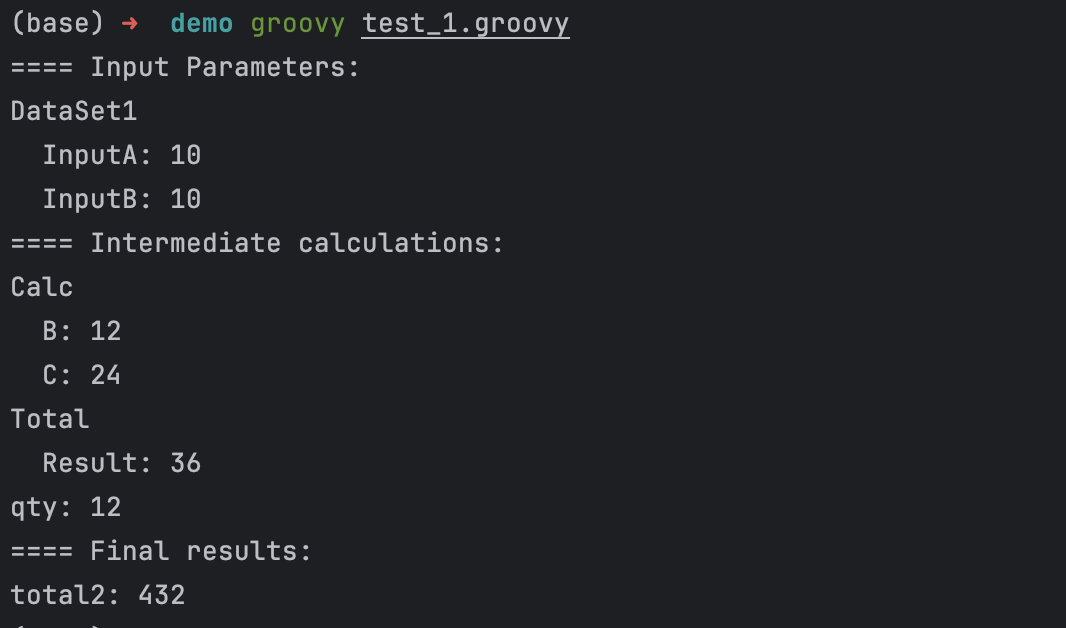
By the way, note that the output of elements in calculate[“Calc”][“B”] is produced in two lines, where the second line is indented. In my solution, the number of such groups reached up to five, and the resulting tree was convenient to read. But more importantly, it was convenient for tracking changes.

Look, you have declared several hundred functions, some of which call others and not just once. And you’ve made some changes somewhere. How to understand what has changed? I did this by comparing the output before and after the edits, and the lines that changed were highlighted for me.

For example, let’s change conf[“X”] from 2 to 3 and compare the program’s output:

It’s also convenient that I can output not the entire tree but only a small part of it starting from a specified element. The calculation is performed at the moment of output, so if other elements are pulled in somewhere, they won’t be displayed, but they will work. For example, instead of prettyPrinter(0, tools.calculate) one can do prettyPrinter(0, tools.calculate[“Calc”]) and it will display B and C for me.

Elements of the structure can be dynamic indexes, and one can iterate over them using each. This allows defining functions immediately for a group, which is specified in the configuration.

This turned out to be very useful:

Of course, the example above is just to illustrate the approach. In my solution, a total of 1039 such constructs were declared. This included all four groups—constants, configuration, intermediate calculations, and final numbers. Each function basically mimicked the Excel formula. The order of the definitions in the modules is not important, because these are definitions, so I could group them by placing “similarly looking”  next to each other. The formulas for different topics share different modules. I could disable some modules to check if there are dependencies on them or not. Disabling means removing it from the function calculate() where we have two modules in our simple app. I had tens in my project. If, after disabling module X, leaving module Y working, the output of the program did not change for me, then this works as a test to verify that Y does not depend on X.

The code above can be found on my github:

https://github.com/raliev/groovy-lazy-calculations